Container with most water
Investigating the problem#
Problem 11 - Container With Most Water
You are given an integer array height of length n.
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
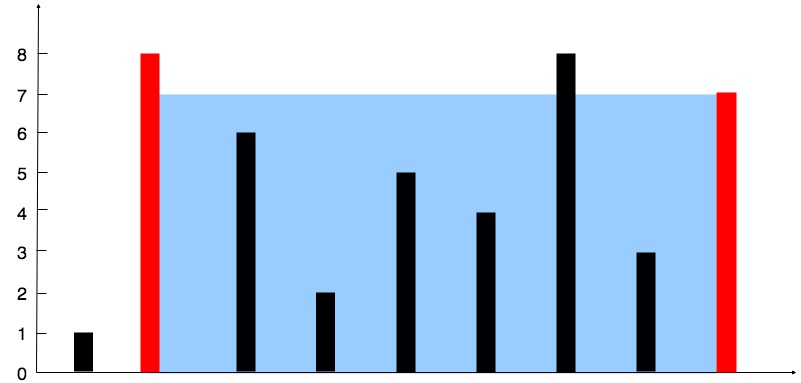
The graph below illustrates the array height = [1,8,6,2,5,4,8,3,7]. The largest area for this array is 49 and can be calculated as follows:
- The two ‘walls’ are created using index 1 (8) and index 8 (7) which are shown in red below
- The area of the container is calculated using the minimum height of the two ‘walls’ (height) multiplied by the difference in index (width)
- This gives us $7 * (8 - 1) = 7 * 7 = 49$
Initial thoughts and prerequisites#
For my solution you will need to know about:
- While loops
- Conditionals
My first idea was that I would have to compare every unique pair of ‘walls’ together and then update a maxArea value when appropriate. Once the loop was finished the value of maxArea could then be returned. There were only a few components to this solution which includes the loop, the calculation of the area, and then a conditional to determine if the value of maxArea should be updated.
To loop through every unique pair I needed two variables. My first idea (which was not optimal) was to have a for loop which iterated through the array, and then utilise a secondary variable and a while loop. This would allow me to
With this method I can find the unique pairs of the array. For example if I had the array height = [1,8,6]. The first pairing would be index 0 (1) and index 1 (8), then each instance with index 0 as the first ‘wall’ would be considered by incrementing the other index. So the second pairing would be index 0 (1) and index 2 (6). Once the second variable reaches the end of the array, it is reset and the first variable is incremented. Therefore, the third pairing would be index 1 (8) and index 2 (6). For the second variable it is more efficient to reset it to its previous value plus one. Otherwise, I would have to repeat some pairings.
Developing the solution#
I first needed to declare variables for the maximum area and the secondary varaible.
maxArea = 0
j = 1
I then needed my for and while loops to be able to get every pairing of ‘walls’. For each pair, the area would need to be calculated and then compared against the current maxArea. Note that I reset the value of the secondary variable to 0 after each while loop originally. As mentioned before this is less efficient since I will be repeating the calculation for some pairs. A better way to do this would be to use a third variable to store the previous starting value of j. Then, when it gets reset, it should be reset to it’s incremented previous value j = prevJ + 1.
for i in range(len(height)):
while (j < len(height)):
area = min(height[i], height[j]) * abs(i-j)
if (area > maxArea):
maxArea = area
j += 1
j = 0
Upon running this solution the final few test cases exceeded the time limit. Therefore, although the code was correct it was not efficient enough. Looking at the complexity of this solution, the main components are the two loops. These are nested and so the time complexity of the code is $O(n^2)$. As such, it was evident that I either needed to make this code more optimised or attempt to create a $O(n)$ time complexity solution.
I first optimised the code by adjusting the value of j to reduce the number of repeated comparisons. This still resulted in the time limit being exceeded and so I thought it would be best to try and take a different approach instead. As I was now quite certain that a $O(n)$ time complexity solution would be required, I knew that I could not rely on any nested loops. This meant that I would need a more intelligent way to search through the pairs of ‘walls’.
As the area is calculated using both the width and the height, I can maximise the width by starting the search from the first index and the last index. Therefore, the first comparison will have the maximum width but not necessarily the largest area as there may be a taller ‘wall’ that would result in a larger area. However, this means the search can be simplified as I can adjust the pointers such that the smaller ‘wall’ being pointed to is changed by either incrementing/decrementing the start/end pointers respectively. This means I can complete one search that ends in the middle of the array, and by that point I will have found the maximum area. Since this only requires one loop this will have a time complexity of $O(n)$.
My two pointers need to point to the start and the end of the array which is achieved as follows:
start = 0
end = len(height) - 1
The loop needs to catch when the entire array has been traversed. Since the starting and ending pointers will be closing in on eachother, I can check for when they overlap which indicates all indexes have been explored. The only other difference is the movement of the pointers which is achieved by adjusting the pointer that points to the smaller wall:
if (height[start] <= height[end]):
start += 1
else:
end -= 1
I now have a complete solution.
Complete solution#
class Solution:
def maxArea(self, height: List[int]) -> int:
maxArea = 0
# Start and end pointers
start = 0
end = len(height) - 1
while (start < end):
# Width * height
area = (end - start) * min(height[start], height[end])
if (area > maxArea):
maxArea = area
# Increment/decrement to iterate over the smaller heights
if (height[start] <= height[end]):
start += 1
else:
end -= 1
return maxArea
Reflection#
This was an enjoyable challenge as it reinforced the idea of the important of efficient code. I am not satisfied with my solution still as I think that it can be condensed and optimised, so this is something I explored. After looking at other solutions in Python, the only key difference seemed to be the use of shorter variable names. I could refactor my solution slightly such that I would not have to use the min() function, but there does not seem to be much benefit in doing so.